week1
第1章节
作业
- A
- A
- A
- D
- D
概念：
监督学习：
有一堆输入并且知道输出(x,y),套用模型得到h,然后根据h来输入新的x得到y
非监督学习：
有一堆输入但不知道输出(x),用程序来进行分类
回归：
输出连续
分类：
输出离散
第2章节
线性回归函数：
一条直线可以拟合数据，没确定之前的函数是
Hypothesis: h_{\theta}(x)=\theta_{0}+\theta_{1} x
现在需要让Hypothesis 去尽可能拟合真实数据，中间会有误差，设一个函数叫代价函数来表示这个误差
代价函数
J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{y}_{i}-y_{i}\right)^{2}=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)^{2}
所有假说函数值和真实y的值相减求和取均值 代价函数越小，拟合越准确
相当于通过 θ0 和 θ1 求 J(θ0, θ1) 的最小值
偏导数
导数代表了在自变量变化趋于无穷小的时候，函数值的变化与自变量变化的比值代表了导数，几何意义有该点的切线。物理意义有该时刻的（瞬时）变化率...
注意在一元函数中，只有一个自变量变动，也就是说只存在一个方向的变化率，这也就是为什么一元函数没有偏导数的原因。
既然谈到偏导数，那就至少涉及到两个自变量，以两个自变量为例，z=f(x,y) . 从导数到偏导数，也就是从曲线来到了曲面. 曲线上的一点，其切线只有一条。但是曲面的一点，切线有无数条
而我们所说的偏导数就是指的是多元函数沿坐标轴的变化率.
f_{x}(x, y)
指的是函数在y方向不变，函数值沿着x轴方向的变化率
f_{y}(x, y)指的是函数在x方向不变，函数值沿着y轴方向的变化率
对应的图像形象表达如下：
-c94a9053c9b342ca989eeeb2185930e6.png)
那么偏导数对应的几何意义是是什么呢？
偏导数f_{x}\left(x_{0}, y_{0}\right)就是曲面被平面
y=y_{0} ,所截得的曲面在点M_{0}处的切线M_{0} T_{x}对x轴的斜率
偏导数f_{y}\left(x_{0}, y_{0}\right)就是曲面被平面x=x_{0}所截得的曲面在点M_{0}处的切线M_{0} T_{y}对y轴的斜率
偏导数指的是多元函数沿坐标轴的变化率，但是我们往往很多时候要考虑多元函数沿任意方向的变化率，那么就引出了方向导数
方向导数
假设你站在山坡上，相知道山坡的坡度（倾斜度）
山坡图如下：
-64ad929245ee4d349b25bbbab184a6fd.png)
假设山坡表示为z=f(x, y),你应该已经会做主要俩个方向的斜率.y方向的斜率可以对y偏微分得到.
同样的，x方向的斜率也可以对x偏微分得到
那么我们可以使用这俩个偏微分来求出任何方向的斜率
（类似于一个平面的所有向量可以用俩个基向量来表示一样）想求出u方向的斜率怎么办
假设z=f(x, y)为一个曲面，p\left(x_{0}, y_{0}\right)为f定义域中一个点，单位向量u=\cos \theta i+\sin \theta j的斜率，
其中\theta是此向量与x轴正向夹角.单位向量u可以表示对任何方向导数的方向.如下图：
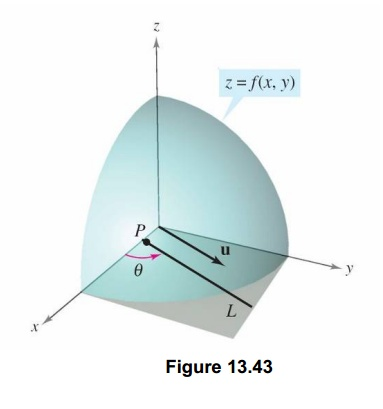
那么我们来考虑如何求出u方向的斜率，可以类比于前面导数定义，得出如下：
设f(x, y)为一个二元函数，u=\cos \theta i+\sin \theta j为一个单位向量，如果下列的极限值存在
\lim _{t \rightarrow 0} \frac{f\left(x_{0}+t \cos \theta, y_{0}+t \sin \theta\right)-f\left(x_{0}, y_{0}\right)}{t}
此方向导数记为D_{u} f则称这个极限值是f沿着u方向的方向导数，那么随着/theta的不同，我们可以求出任意方向的方向导数.这也表明了方向导数的用处，是为了给我们考虑函数对任意方向的变化率.
在求方向导数的时候，除了用上面的定义法求之外，我们还可以用偏微分来简化我们的计算.
表达式是：D_{u} f(x, y)=f_{x}(x, y) \cos \theta+f_{y}(x, y) \sin \theta（至于为什么成立，很多资料有，不是这里讨论的重点）
那么一个平面上无数个方向，函数沿哪个方向变化率最大呢？
目前我不管梯度的事，我先把表达式写出来：
\begin{aligned}
&D_{u} f(x, y)=f_{x}(x, y) \cos \theta+f_{y}(x, y) \sin \theta\\
&\text { 设 } A=\left(f_{x}(x, y), f_{y}(x, y)\right), I=(\cos \theta, \sin \theta)
\end{aligned}
那么我们可以得到：
D_{u} f(x, y)=A \bullet I=|A| *|I| \cos \alpha(\alpha \text { 为向量 } A \text { 与向量 } I \text { 之间的夹角 })
那么此时如果D_{u} f(x, y)要取得最大值，也就是当\alpha为0度的时候
也就是向量I（这个方向是一直在变，在寻找一个函数变化最快的方向）与向量A（这个方向当点固定下来的时候，它就是固定的）平行的时候，方向导数最大.方向导数最大，也就是单位步伐，函数值朝这个反向变化最快.
好了，现在我们已经找到函数值下降最快的方向了，这个方向就是和A向量相同的方向.那么此时我把A向量命名为梯度（当一个点确定后，梯度方向是确定的），也就是说明了为什么梯度方向是函数变化率最大的方向了！！！（因为本来就是把这个函数变化最大的方向命名为梯度）
我的理解是，本来梯度就不是横空出世的，当我们有了这个需求（要求一个方向，此方向函数值变化最大），得到了一个方向，然后这个方向有了意义，我们给了它一个名称，叫做梯度
梯度
- 梯度的提出只为回答一个问题： 函数在变量空间的某一点处，沿着哪一个方向有最大的变化率？
- 梯度定义如为：函数在某一点的梯度是这样一个 向量，它的方向是在所有方向导数中，最大的方向导数的方向，它的模为方向导数的最大值。
- 也可以这么理解：梯度即函数在某一点最大的方向导数，沿梯度方向，函数具有最大的变化率。
梯度下降
从一组参数值（θ0, θ1）开始，不断地去尝试各种（θ0, θ1），直到使得代价函数 J(θ0, θ1) 最小为止，凸函数只有一个全局最优解，其它还会有局部最优解
repeat until convergence{
\left.\theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{i}} J\left(\theta_{0}, \theta_{1}\right) \quad \text { (for } j=0 \text { and } j=1\right)
}
该函数每次循环都要将 θ0, θ1 更新，并且保证同步更新
\begin{aligned}
&\operatorname{temp} 0:=\theta_{0}-\alpha \frac{\partial}{\partial \theta_{0}} J\left(\theta_{0}, \theta_{1}\right)\\
&\operatorname{tem} p 1:=\theta_{1}-\alpha \frac{\partial}{\partial \theta_{1}} J\left(\theta_{0}, \theta_{1}\right)\\
&\theta_{0}:=\operatorname{tem} \mathrm{p} 0\\
&\theta_{1}:=\text { temp } 1
\end{aligned}
是一个循环结构，当不能再更新 θ0, θ1 时循环停止，:= 是一个赋值号，α 是学习速率，也就是你下山每次迈出多大步子，后面紧跟着的是一个偏导数。这个偏导数我们用一种最简单的情况来解释，就令 θ0=0，现在就剩下 θ1
\theta_{1}:=\theta_{1}-\alpha \frac{d}{\alpha\theta_1} J\left(\theta_{1}\right)
函数右边a是速度再右边是求导（斜率）越接近局部最优解越小，所以不用刻意减小速度,下降到局部最小处时，导数恰好为0，就不会再更新了，学习速率 α如果太大，快接近局部最优解的时候就会跳过去，收敛不了，离散了
线性回归梯度下降
利用梯度下降法来求代价函数的局部最优解
作业
- 4
- E
- 3
- A B C D
- B D
第三章节
向量是只有一列的矩阵（nx1）
作业
- B
- B
- C
- 10
- A B
